Số nguyên tố
Số nguyên tố là số tự nhiên chỉ có các ước số là 1 và chính nó. Các số có nhiều hơn 2 ước số được gọi là hợp số. [1]
Do 1 chỉ có 1 ước số là chính nó, nên 1 không phải là số nguyên tố và cũng không phải là hợp số.
Mục lục
Danh sách[sửa | sửa mã nguồn]
Các số nguyên tố từ 2 đến 100:
Số 2 là số nguyên tố nhỏ nhất, và cũng là số nguyên tố chẵn duy nhất.
Tính chất[sửa | sửa mã nguồn]
Ký hiệu "b  a" nghĩa là b là ước của a, ký hiệu a
a" nghĩa là b là ước của a, ký hiệu a  b nghĩa là a chia hết cho b.
b nghĩa là a chia hết cho b.
1. Ước tự nhiên khác 1 nhỏ nhất của một số tự nhiên là số nguyên tố.
Chứng minh: Giả sử d  a; d nhỏ nhất; d
a; d nhỏ nhất; d  1.
1.
Nếu d không nguyên tố  d = d1.d2; d1, d2 > 1
d = d1.d2; d1, d2 > 1
 d1|a với d1 < d: mâu thuẫn với d nhỏ nhất. Vậy d là nguyên tố.
d1|a với d1 < d: mâu thuẫn với d nhỏ nhất. Vậy d là nguyên tố.
2. Cho p là số nguyên tố; a  N; a
N; a  0. Khi đó
0. Khi đó
- (a,p) = p
 (a
(a p)
p) - (a,p) = 1
 (a
(a p)
p)
3. Nếu tích của nhiều số chia hết cho một số nguyên tố p thì có ít nhất một thừa số chia hết cho p.
-

 p
p 
 ai
ai  p
p
4. Ước số dương bé nhất khác 1 của một hợp số a là một số nguyên tố không vượt quá 
5. 2 là số nguyên tố nhỏ nhất và cũng là số nguyên tố chẵn duy nhất
6. Tập hợp các số nguyên tố là vô hạn (tương đương với việc không có số nguyên tố lớn nhất).
Chứng minh: Giả sử có hữu hạn số nguyên tố: p1 < p2 <... < pn
Xét a = p1.p2.... pn + 1
Ta có: a > 1 và a ¹ pi; "i = Þ a là hợp số Þ a có ước nguyên tố pi,
hay aMpi và (pi) M pi Þ 1M pi: mâu thuẫn.
Vậy tập hợp các số nguyên tố là vô hạn.
Bảng số nguyên tố-sàng Eratosthene[sửa | sửa mã nguồn]
Sàng Eratosthene[sửa | sửa mã nguồn]
Sàng Eratosthenes là một giải thuật cổ xưa để lập bảng tất cả các số nguyên tố nhỏ hơn một số n cho trước. Giải thuật dựa trên tính chất: mọi hợp số n đều có ước nguyên tố không vượt quá căn của chính nó (sqrt(n)). Giải thuật đầu tiên xóa số 1 ra khỏi tập các số nguyên tố. Số tiếp theo số 1 là số 2, là số nguyên tố. Bắt đầu từ số 2 xoá tất cả các bội của 2 ra khỏi bảng. Số đầu tiên không bị xoá sau số 2 (số 3) là số nguyên tố. Tiếp theo lại xoá các bội của 3... Giải thuật tiếp tục cho đến khi găp số nguyên tố lớn hơn hoặc bằng sqrt(n) thì dừng lại. Tất cả các số chưa bị xoá là số nguyên tố. Theo ngôn ngữ thuật toán ta có thể diễn đạt giải thuật sàng Eratosthene như sau:
Eratosthene(n)
Var List Prime[1..n]
Int i,j,k
for i:=1 to n Prime[i]:=True
Prime[1]:=false
k=0
while k < sqrt(n) {
i=k+1
while Prime[i]=False i:=i+1
k=i
j=2
while k*j<=n {
Prime[k*j]:= False
j:=j+1
}
}
Lịch sử các bảng số nguyên tố[sửa | sửa mã nguồn]
Định lý cơ bản của số học[sửa | sửa mã nguồn]
Phát biểu định lý: "Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích những thừa số nguyên tố, và sự phân tích này là duy nhất nếu không kể đến thứ tự của các thừa số."
Từ đó có dạng phân tích tiêu chuẩn của một số tự nhiên bất kỳ là:
Trong đó p1,p2,...,pm, là các số nguyên tố đôi một khác nhau. Ta có n chia hết cho (k1+1)(k2+1)...(km+1) số tự nhiên. Ví dụ:
300 chia hết cho (2+1)(2+1)(1+1)=18 số tự nhiên.
Đây cũng là công thức tính số các ước của số tự nhiên n: Số các ước = (k1+1)(k2+1)...(km+1).
Số nguyên tố Fermat và Mersenne[sửa | sửa mã nguồn]
Xem bài viết ở:
Số nguyên tố lớn nhất[sửa | sửa mã nguồn]
- Giả thiết 1: Không có số nguyên dương X nào là số nguyên tố lớn nhất, nghĩa là không tồn tại số mà các số lớn hơn nó Y>X sẽ buộc phải chia hết cho các số nguyên nhỏ hơn hoặc bằng X
- Giả thiết 2: số vô cùng lớn ∞ không thể xác định là số nguyên tố hay hợp số
- Giả thiết 3: Lực lượng của tập hợp số nguyên tố là vô hạn đếm được
Với 3 giả thiết trên thì việc xác định số nguyên tố lớn nhất là không thể được; tuy nhiên, với khả năng tính toán của máy tính, người ta có thể tính ra được số nguyên tố (số nguyên chắc chắn là số nguyên tố) lớn nhất tính được đến tháng 1 năm 2013 là số nguyên tố Mersenne thứ 48 với 17,425,170 chữ số[3]:
- 2^57,885,161 - 1
Giả thiết Goldbach - Euler[sửa | sửa mã nguồn]
Năm 1742, nhà toán học Đức Christian Goldbach viết thư cho Euler biết rằng ông mạo hiểm đưa ra bài toán: Mọi số tự nhiên lớn hơn 5 đều biểu diễn được dưới dạng tổng của 3 số nguyên tố. Euler trả lời rằng theo ông, mọi số chẵn lớn hơn 2 đều biểu diễn được dưới dạng tổng của 2 số nguyên tố. Nếu chứng minh được một trong hai mệnh đề thì sẽ chứng minh được mệnh đề còn lại. 200 năm sau, đến năm 1937, nhà toán học Liên Xô Vinogradov đã giải quyết gần trọn vẹn bài toán đó bằng cách chứng minh rằng mọi số lẻ đủ lớn đều có thể biểu diễn được dưới dạng tổng của 3 số nguyên tố.
Cho đến nay, bài toán Goldbach-Euler vẫn chưa giải được hoàn toàn. Nếu mệnh đề của Euler là đúng, hãy chứng minh mệnh đề Goldbach. Giải: Cho số tự nhiên n>5, ta sẽ chứng minh rằng n viết được dưới dạng tổng của 3 số nguyên tố. Xét:
- Trường hợp 1: Nếu n chẵn thì n=2+m với m chẵn, m>3. vì số chẵn >2 kế tiếp là 4 nên dù là m>3 thì m vẫn viết được dưới dạnng tổng 2 số nguyên tố.
- Trường hợp 2: nếu n lẻ thì n=3+m với m chẵn, m>2. Theo mệnh đề Euler, m chẵn, m>2 nên m viết được dưới dạng tổng hai số nguyên tố. Do đó n viết được dưới dạng tổng của 3 số nguyên tố.
Chú thích[sửa | sửa mã nguồn]
- ^ Số nguyên tố, Từ điển toán học thông dụng trang 445, Tác giả Ngô Thúc Lanh, Đoàn Quỳnh, Nguyễn Đình Trí, Nhà xuất bản giáo dục, in năm 2000
- ^ (dãy A000040 trong OEIS).
- ^ Số nguyên tố Mersenne thứ 48
- Số tự nhiên
- Số chẳn
- Số lẻ
- Số nguyên
- Phân số
- Số vô tỷ
- Số hữu tỷ
- Số phức
- Số nguyên Gauss
- Số nguyên Eisenstein
- Số vô tỷ Quadratic
- Căn của đơn vị
- Gaussian period
- Số Pisot-Vijayaraghavan
- Số Salem
Liên kết ngoài[sửa | sửa mã nguồn]
- Trang web số nguyên tố
- Lịch sử nghiên cứu số nguyên tố
- Prime Number Generator - Generate a given number of primes above a given start number.
- 15, 000, 000 số nguyên tố đầu tiên
- The prime puzzles
- Phiên bản tiếng Anh của định lý Euclid về giới hạn số nguyên tố
- Số nguyên tố trên WIMS
- Vòng số với họa tiết tạo bởi phân bố số nguyên tố
- An Introduction to Analytic Number Theory, by Ilan Vardi and Cyril Banderier
- Factorizer Windows software to find prime numbers and pairs of prime numbers less than 2.147.483.646.
- A fast, downloadable prime number calculator written in Visual Basic 6
| Wikimedia Commons có thêm thư viện hình ảnh và phương tiện truyền tải về Số nguyên tố |
 (a
(a p)
p)

 ai
ai 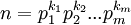












0 nhận xét:
Đăng nhận xét